If X is a random vector
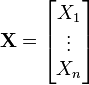 ,
,the covariance matrix is
![\Sigma
= \begin{bmatrix}
\mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \\
\mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
\mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)]
\end{bmatrix}.](http://upload.wikimedia.org/math/5/8/5/58572fa5b05e778f5a5eff9ec1b3ddb6.png)
Det(\(\Sigma\)) = \(\prod_{i=1}^n\lambda_i \geq 0\) where \(\lambda_i\)'s are eigenvalues of \(\Sigma\).
Since \(\Sigma\) is symmetric and positive definite, it can be diagonalized and its eigenvalues are all real and positive and the eigenvectors are orthogonal.
\begin{align}
det(\Sigma) = det(V\Lambda V^T) = det(V)\cdot det(\Lambda) \cdot det(V^T) = det(\Lambda)
\end{align}
\(det(V) = \pm 1\) because \(det(VV^{-1}) = det(V)det(V^{-1}) = det(V)det(V^T) = det(V)^2 = 1\)
References:
http://www.ece.unm.edu/faculty/bsanthan/EECE-541/covar.pdf
No comments:
Post a Comment