Covariance matrix

If X is a random vector
 ,
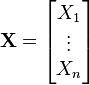the covariance matrix is




Det(\(\Sigma\)) = \(\prod_{i=1}^n\lambda_i \geq 0\) where \(\lambda_i\)'s are eigenvalues of \(\Sigma\).

Since \(\Sigma\) is symmetric and positive definite, it can be diagonalized and its eigenvalues are all real and positive and the eigenvectors are orthogonal.
\begin{align}
det(\Sigma) = det(V\Lambda V^T) = det(V)\cdot det(\Lambda) \cdot det(V^T) = det(\Lambda)
\end{align}

\(det(V) = \pm 1\) because \(det(VV^{-1}) = det(V)det(V^{-1}) = det(V)det(V^T) = det(V)^2 = 1\)

References:
http://www.ece.unm.edu/faculty/bsanthan/EECE-541/covar.pdf